Area of a Parallelogram

Lesson Objective

In this lesson, we will learn about the area of a parallelogram.

About This Lesson

In this lesson, we will:

Learn about the formula for the area of a parallelogram
See an example on using the formula to calculate a parallelogram's area
See another example on using the formula to calculate the height of a parallelogram

The study tips and math video below will explain more.

Study Tips

Tip #1

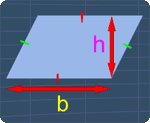
A parallelogram has two pairs of parallel sides and its opposite sides are equal in length. These properties are shown on the right.

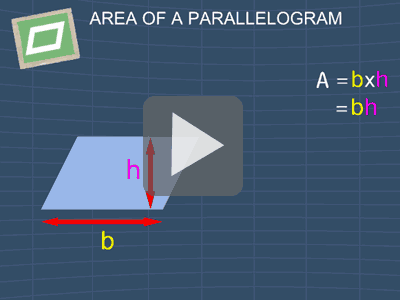
Now, if the parallelogram has the base b and the height h, the area, A, of the parallelogram will be:

A = bh

a parallelogram has 2 pairs of parallel sides

a parallelogram with the base b and height h. Its opposite sides are equal in length.

The math video below will give more explanations on this. Also, we will see some examples on how to use this formula.

Math Video

Lesson Video

Math Video Transcript

00:00:03.170
In this lesson, we will learn about the area of a parallelogram.

00:00:08.120
Consider this parallelogram with the base B and the height H.

00:00:14.190
Now, to find the area of this parallelogram, A, let's observe this parallelogram carefully.

00:00:22.060
If we cut out this portion and place it here. Observe that, we now have a rectangle. 

00:00:30.150
Therefore, we can say that the area of this parallelogram is that same as, the area of this rectangle.

00:00:38.050
In the previous lesson, we learned that the area of a rectangle can be found by multiplying its length and width together.

00:00:46.240
Similarly, we can find this area, by multiplying the base, and height together. Hence, we have B multiply H which is the same as BH.  

00:00:59.180
Let's change this back to a parallelogram. Now, the area of this parallelogram, A, equals to BH.

00:01:09.210
Note that, it is very important to include the unit. Since this is the formula for area, its unit will be in the form of square unit.

00:01:19.160
We will see more explanations on this, in the upcoming example.

00:01:25.020
Now, let's see some examples on using this formula.

00:01:29.220
Find the area of this parallelogram when its base is 5cm, and its height is 3cm.

00:01:37.110
To solve this, we start with the formula for the area of a parallelogram, A equals to BH.

00:01:44.240
Since the base is given as 5cm, we can substitute b with 5.

00:01:51.010
Similarly, since the height is given as 3cm, we can substitute h with 3.

00:01:57.240
Next, we can simplify by multiplying 5 with 3. This gives 15.

00:02:05.020
Note that, this number has no meaning unless we include the unit for it.

00:02:10.070
Since the units are given in centimeter, the unit for the area will be in square centimeter.

00:02:16.070
Hence, the area of this parallelogram is 15 square centimeter.

00:02:22.240
Next example, given that the area of this parallelogram is 20 square feet, and its base is 4ft. Find its height.

00:02:32.130
Again, we start with the formula for the area of a parallelogram, A equals to BH.

00:02:39.190
Now, since the area, and the base are given, we can find the height by solving this equation for H. Here’s how.

00:02:48.210
Since the area is given as 20 square feet, we can substitute A with 20.

00:02:54.210
Similarly, since the base is given as 4cm, we can substitute b with 4.

00:03:01.220
Now we have, 4H equals to 20.

00:03:06.080
Let's rewrite this equation so that it will look neater.

00:03:10.120
To find h, we need to remove 4. We can do so by dividing both sides of the equation with 4.

00:03:19.070
By doing so, we have, H equals to 20 over 4.

00:03:25.090
20 divides by 4, gives 5.

00:03:29.040
Now, this number is meaningless unless we include the unit for it.

00:03:34.030
Since the base is in feet, the height of the parallelogram will be in feet.

00:03:40.000
Therefore, the height of this parallelogram is 5 ft.

00:03:45.220
That is all for this lesson. Try out the practice question to further your understanding.

Practice Questions & More

Multiple Choice Questions (MCQ)

Now, let's try some MCQ questions to understand this lesson better.

You can start by going through the series of questions on the area of a parallelogram or pick your choice of question below.

Question 1 on finding the area of a parallelogram
Question 2 on finding the height of a parallelogram

Return to Home Page