
Exponent Law Practice Question

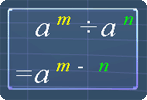



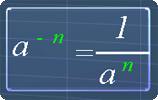
Question 1
Which of the following equations are true?
I. (ab)0 = 1
II. (a2b)3 = a5b3
III. (a10b-3)0 = z0
The following pictures are the exponent laws. You can use them as reference.
I. (ab)0 = 1
II. (a2b)3 = a5b3
III. (a10b-3)0 = z0
The following pictures are the exponent laws. You can use them as reference.
Answer
Select and check your answer...
Check Answer
Step by Step Solution
Step 1
Let's take a look at: I. (ab)0 = 1
We can treat ab as 'some number'. So, this term becomes:
(some number)0
Referring to the law as shown in the picture, we can see that (some number)0 is equals to 1.
Therefore, I. is true.
We can treat ab as 'some number'. So, this term becomes:
(some number)0
Referring to the law as shown in the picture, we can see that (some number)0 is equals to 1.
Therefore, I. is true.

Step 2
Let's take a look at: II. (a2b)3 = a5b3
Oops! It seems that (a2b)3 doesn't fit into the exponent law as shown in the picture.
However, if we understand the logic behind the exponent laws, we can derive our own formula.
The following step will show you how.
Oops! It seems that (a2b)3 doesn't fit into the exponent law as shown in the picture.
However, if we understand the logic behind the exponent laws, we can derive our own formula.
The following step will show you how.
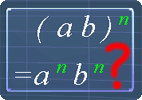
Step 3
Now, we know that:
(a2b)3 = (a2b)(a2b)(a2b)
= a6b3
Now, realize that you can also get a6b3 by:
a6b3 = a2x3 b1x3
With this, we can see that: (a2b1)3 = a2x3 b1x3
Therefore, we can formulate: (anbm)p = anp bmp
*Note that b = b1
(a2b)3 = (a2b)(a2b)(a2b)
= a6b3
Now, realize that you can also get a6b3 by:
a6b3 = a2x3 b1x3
With this, we can see that: (a2b1)3 = a2x3 b1x3
Therefore, we can formulate: (anbm)p = anp bmp
*Note that b = b1
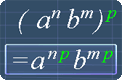
Step 4
Anyway, since we already found that:
(a2b)3 = a6b3
The equation II. (a2b)3 = a5b3 is false.
(a2b)3 = a6b3
The equation II. (a2b)3 = a5b3 is false.
Step 5
Let's take a look at:
III. (a10b-3)0 = z0
Again, we can treat a10b-3 as 'some number'. So this term becomes:
(some number)0
Referring to the law as shown in the picture, we can see that (some number)0 is equals to 1.
Now, z0 is also equals to 1. So, the equation becomes: 1 = 1
Therefore, III. is true.
Again, we can treat a10b-3 as 'some number'. So this term becomes:
(some number)0
Referring to the law as shown in the picture, we can see that (some number)0 is equals to 1.
Now, z0 is also equals to 1. So, the equation becomes: 1 = 1
Therefore, III. is true.

Step 6
From Step 1 to Step 5. The valid choices
are I and III.
Clearly, the answer is B.
Clearly, the answer is B.
To close all the steps, reload the exponent law practice question page