X and Y Intercept

Lesson Objective

This lesson shows what x and y intercepts. Also, you will see some examples on how to find the intercepts of linear equations.

About This Lesson

The ideas behind x-intercept and y-intercept are quite simple.

This lesson will show you the important ideas that you must understand about x and y intercepts. Also, you will get to see some examples on find them.

You can proceed by reading the study tips first or watch the math video or try out the practice questions.

Study Tips

Tip #1

This lesson involves solving linear equation. If you need to recall on how to solve linear equations, you can watch the math videos in:

Tip #2

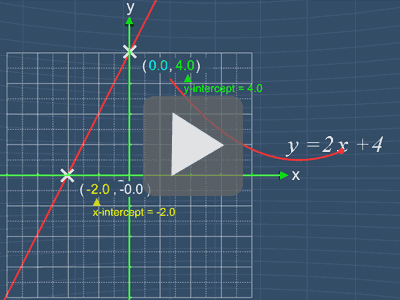
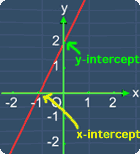
As you can guess, the x-intercept is referring to the x-coordinate of the point where the graph crosses the x-axis.

Similarly, the y-intercept is referring to the
y-coordinate of the point where the graph crosses the y-axis.

Now, watch the following math video to learn more.

Math Video

Click play to watch video

Math Video Transcript

00:00:01.180
This lesson shows you what are x and y intercepts and how to find them.

00:00:06.230
Now, consider this line. Notice that, this line crosses the y-axis and x-axis. 

00:00:15.210
As you can see,  the coordinates of the point that the line crosses the y-axis is (0.0, 3.0).

00:00:25.070
Now, the y-intercept is simply the y-coordinate of the point where the line crosses the y-axis. 

00:00:31.090
Therefore, the y-intercept of this line is 3.0.

00:00:37.010
Alright, when I move this point along the y-axis, notice how the y-intercept changes.

00:00:46.010
More importantly, notice the x-coordinate always remains as 0.0. 

00:00:54.140
Next, let's take a look at x-intercept.

00:00:58.240
The coordinates of the point that the line crosses the x-axis is (4.0,0.0).

00:01:06.050
Now, the x-intercept is simply the x-coordinate of the point where the line crosses the x-axis. 

00:01:11.210
Therefore, the x-intercept of this line is 4.0.

00:01:16.230
Alright, when I move this point along the x-axis, notice how the x-intercept changes.

00:01:26.040
Also, notice that the y-coordinates remains as 0.0. 

00:01:33.220
That's all we need to know about x and y intercept. 

00:01:37.000
Now, let's look at some examples on how to find x and y intercept, and draw the line for the given equation.

00:01:44.000
Now, given the equation, y = 2x+4. Let's first find the y-intercept of this line.

00:01:52.000
We know that the y-intercept, is the y-coordinate of the point where the line crosses the y-axis.

00:01:58.100
Since we do not know the coordinates of this point, let's just put a point on the y-axis with the coordinates (0,y). 

00:02:06.170
Now, this y-coordinate, is the y-intercept that we are going to find.

00:02:11.240
Logically, to calculate y, we need to know the value of x.  

00:02:17.180
So, what is the value of x? It is Zero!. 

00:02:20.220
This is because the x-coordinate of any point on the y-axis is always zero.

00:02:26.110
Therefore, we can substitute x with 0.

00:02:30.180
To find y, multiply 2 with 0 gives 0. 0 plus 4 gives 4. So, we get have the y-intercept as 4.

00:02:43.190
Let's adjust this point to the correct coordinates.

00:02:48.090
Next, let's find the x-intercept.

00:02:52.140
Now, we know that the x-intercept, is the x-coordinate of the point where the line crosses the x-axis.

00:03:00.060
Since we do not know the coordinates of this point, let's just put a point on the x-axis with the coordinates (x,0). 

00:03:08.240
Now, this x-coordinate, is the x-intercept that we are going to find.

00:03:14.190
Now, to find x, we need to know is the value of y.  

00:03:20.050
So what is the value of y? It is Zero!. 

00:03:22.070
This is because the y-coordinate of any point on the x-axis is always zero.

00:03:28.030
Therefore, we can substitute y with 0.

00:03:31.210
To find x, we add -4 to both sides of the equation. 

00:03:37.140
This gives 0 - 4 = 2x. Now,  0 minus 4 gives -4.

00:03:46.050
Next, we divide both sides of the equation by  with, 2. Hence, we have -4/2 = x. 

00:03:55.100
-4 divides by 2 gives - 2. Finally, we get the x-intercept as -2.

00:04:04.110
Let's adjust this point to the correct coordinates.

00:04:10.120
With these 2 points, we can now draw the line, y = 2x +4.

00:04:18.220
Next example, find the x and y intercept, and draw the line of 2x-4y = 8. 

00:04:27.120
Let's first find the y-intercept. Substituting x with 0. 

00:04:34.040
Since 2 multiply by 0 gives 0, we can just remove this term.

00:04:41.080
Now, to solve for y, we divide - 4 to both sides of the equation. 

00:04:47.060
This gives y equals to, 8 divides by - 4. 8 divides by  -4 gives  -2. 

00:04:56.060
So we have the y-intercept as -2. 

00:05:00.160
Let's adjust this point to the correct coordinates.

00:05:06.130
Next, let's find the x-intercept. Substituting y with 0. Since -4 multiply by 0 gives 0, we can just remove this term.


00:05:21.040
Now, to solve for x, we divides both sides of the equation with 2.  This gives x = 8/2. 

00:05:31.090
8 divides by 2 gives  4. 

00:05:34.240
So we have the x-intercept as  4. Let's adjust this point to the correct coordinates.

00:05:43.000
With these 2 points, we can now draw the line of 2x-4y = 8.

00:05:50:000
That is all for this lesson. Try out the practice question to test your understanding.

Practice Questions & More

Multiple Choice Questions (MCQ)

Now, let's try some MCQ questions to understand this lesson better.

You can start by going through the series of questions on x and y intercept or pick your choice of question below.

Question 1 on finding x and y intercepts.
Question 2 on finding x and y intercepts for a quadratic graph

Return to Home Page