Khan Academy on a Stick
Divergence theorem
Divergence theorem intuition. Divergence theorem examples and proofs. Types of regions in 3D.
-
 3-D Divergence Theorem Intuition
3-D Divergence Theorem Intuition
Intuition behind the Divergence Theorem in three dimensions
-
 Divergence Theorem Example 1
Divergence Theorem Example 1
Example of calculating the flux across a surface by using the Divergence Theorem
-
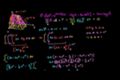 Why we got zero flux in Divergence Theorem Example 1
Why we got zero flux in Divergence Theorem Example 1
Intuition as to why we go no net flux in the last worked example
Divergence theorem (3D)
An earlier tutorial used Green's theorem to prove the divergence theorem in 2-D, this tutorial gives us the 3-D version (what most people are talking about when they refer to the "divergence theorem"). We will get an intuition for it (that the flux through a close surface--like a balloon--should be equal to the divergence across it's volume). We will use it in examples. We will prove it in another tutorial.
-
 Type I Regions in Three Dimensions
Type I Regions in Three Dimensions
Definition of Type 1 regions. Visualizing what is and isn't a Type I region
-
 Type II Regions in Three Dimensions
Type II Regions in Three Dimensions
Definition and intuition for Type 2 Regions
-
 Type III Regions in Three Dimensions
Type III Regions in Three Dimensions
Definition and intuition for type 3 regions
Types of regions in three dimensions
This tutorial classifies regions in three dimensions. Comes in useful for some types of double integrals and we use these ideas to prove the divergence theorem.
-
 Divergence Theorem Proof (part 1)
Divergence Theorem Proof (part 1)
Setting up the proof for the divergence theorem
-
 Divergence Theorem Proof (part 2)
Divergence Theorem Proof (part 2)
Breaking up the surface integral
-
 Divergence Theorem Proof (part 3)
Divergence Theorem Proof (part 3)
Evaluating the surface integral
-
 Divergence Theorem Proof (part 4)
Divergence Theorem Proof (part 4)
More evaluation of the surface integral
-
 Divergence Theorem Proof (part 5)
Divergence Theorem Proof (part 5)
Home stretch. Proving the Type I part
Divergence theorem proof
You know what the divergence theorem is, you can apply it and you conceptually understand it. This tutorial will actually prove it to you (references types of regions which are covered in the "types of regions in 3d" tutorial.