Khan Academy on a Stick : Line integrals and Green's theorem

Khan Academy on a Stick

Calculus

Limits
Taking derivatives
Derivative applications
Indefinite and definite integrals
Solid of revolution
Sequences, series and function approximation
Double and triple integrals
Partial derivatives, gradient, divergence, curl
Line integrals and Green's theorem
Surface integrals and Stokes' theorem
Divergence theorem

Introduction to the Line Integral
cc

Introduction to the Line Integral
Line Integral Example 1
cc

Concrete example using a line integral
Line Integral Example 2 (part 1)
cc

Line integral over a closed path (part 1)
Line Integral Example 2 (part 2)
cc

Part 2 of an example of taking a line integral over a closed path

Line integrals for scalar functions

With traditional integrals, our "path" was straight and linear (most of the time, we traversed the x-axis). Now we can explore taking integrals over any line or curve (called line integrals).

Position Vector Valued Functions
cc

Using a position vector valued function to describe a curve or path
Derivative of a position vector valued function
cc

Visualizing the derivative of a position vector valued function
Differential of a vector valued function
cc

Understanding the differential of a vector valued function
Vector valued function derivative example
cc

Concrete example of the derivative of a vector valued function to better understand what it means

Position vector functions and derivatives

In this tutorial, we will explore position vector functions and think about what it means to take a derivative of one. Very valuable for thinking about what it means to take a line integral along a path in a vector field (next tutorial).

Line Integrals and Vector Fields
cc

Using line integrals to find the work done on a particle moving through a vector field
Using a line integral to find the work done by a vector field example
cc

Using a line integral to find the work done by a vector field example
Parametrization of a Reverse Path
cc

Understanding how to parametrize a reverse path for the same curve.
Scalar Field Line Integral Independent of Path Direction
cc

Showing that the line integral of a scalar field is independent of path direction
Vector Field Line Integrals Dependent on Path Direction
cc

Showing that, unlike line integrals of scalar fields, line integrals over vector fields are path direction dependent
Path Independence for Line Integrals
cc

Showing that if a vector field is the gradient of a scalar field, then its line integral is path independent
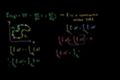Closed Curve Line Integrals of Conservative Vector Fields
cc

Showing that the line integral along closed curves of conservative vector fields is zero
Example of Closed Line Integral of Conservative Field
cc

Example of taking a closed line integral of a conservative field
Second Example of Line Integral of Conservative Vector Field
cc

Using path independence of a conservative vector field to solve a line integral

Line integrals in vector fields

You've done some work with line integral with scalar functions and you know something about parameterizing position-vector valued functions. In that case, welcome! You are now ready to explore a core tool math and physics: the line integral for vector fields. Need to know the work done as a mass is moved through a gravitational field. No sweat with line integrals.

Green's Theorem Proof Part 1
cc

Part 1 of the proof of Green's Theorem
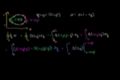Green's Theorem Proof (part 2)
cc

Part 2 of the proof of Green's Theorem
Green's Theorem Example 1
cc

Using Green's Theorem to solve a line integral of a vector field
Green's Theorem Example 2
cc

Another example applying Green's Theorem

Green's theorem

It is sometimes easier to take a double integral (a particular double integral as we'll see) over a region and sometimes easier to take a line integral around the boundary. Green's theorem draws the connection between the two so we can go back and forth. This tutorial proves Green's theorem and then gives a few examples of using it. If you can take line integrals through vector fields, you're ready for Mr. Green.

Constructing a unit normal vector to a curve
cc

Figuring out a unit normal vector at any point along a curve defined by a position vector function
2 D Divergence Theorem
cc

Using Green's Theorem to establish a two dimensional version of the Divergence Theorem
Conceptual clarification for 2-D Divergence Theorem
cc

Understanding the line integral as flux through a boundary

2-D Divergence theorem

Using Green's theorem (which you should already be familiar with) to establish that the "flux" through the boundary of a region is equal to the double integral of the divergence over the region. We'll also talk about why this makes conceptual sense.