
Exponent Laws Questions

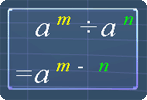



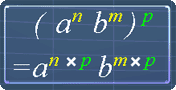
Question 2
Simplify the following expression:

The following pictures are the exponent laws. You can use them as reference.

The following pictures are the exponent laws. You can use them as reference.
Answer
Select and check your answer...
Check Answer
Step by Step Solution
Step 1
Let's first focus on the numerator:
6(q2s3)2
Using the exponent law* as shown in the picture, we get:
6(q2s3)2 = 6q2 x 2 s3 x 2
*Note: If you are not sure on how to derive this law, you can see it at step 3 in this practice question.
6(q2s3)2
Using the exponent law* as shown in the picture, we get:
6(q2s3)2 = 6q2 x 2 s3 x 2
*Note: If you are not sure on how to derive this law, you can see it at step 3 in this practice question.
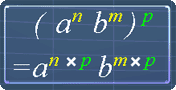

Step 2
Now,
2 multiply by 2 gives 4, and
3 multiply by 2 gives 6.
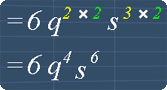
Hence, we have 6q4s6.
2 multiply by 2 gives 4, and
3 multiply by 2 gives 6.
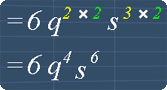
Hence, we have 6q4s6.
Step 3
Next, let's focus on the denominator:
2(qs2)3
Using the exponent law* as shown in the picture, we get:
2(qs2)3 = 2q1 x 3 s2 x 3
*Note: If you are not sure on how to derive this law, you can see it at step 3 in this practice question.
2(qs2)3
Using the exponent law* as shown in the picture, we get:
2(qs2)3 = 2q1 x 3 s2 x 3
*Note: If you are not sure on how to derive this law, you can see it at step 3 in this practice question.
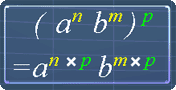
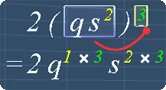
Step 4
Now,
1 multiply by 3 gives 3, and
2 multiply by 3 gives 6.
Hence, we have 2q3s6.
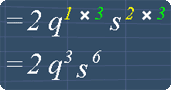
1 multiply by 3 gives 3, and
2 multiply by 3 gives 6.
Hence, we have 2q3s6.
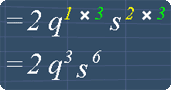
Step 5
Now, after simplifying the numerator and denominator, the original expression becomes:
6q4s6 ÷ 2q3s6
6q4s6 ÷ 2q3s6
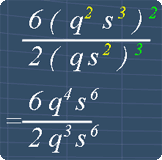
Step 6
Using the exponent law as shown in the picture, we get:
6q4s6 ÷ 2q3s6
= 3q4 - 3 s6 - 6
6q4s6 ÷ 2q3s6
= 3q4 - 3 s6 - 6
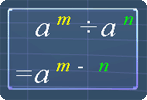
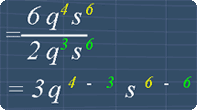
Step 7
Simplifying,
3q4 - 3 s6 - 6
We get:
3q1 s0
Now, we can write:
q1 as q and,
s0 as 1
3q4 - 3 s6 - 6
We get:
3q1 s0
Now, we can write:
q1 as q and,
s0 as 1

Step 8
Finally, we have the simplest term, 3q.
Clearly, the answer is C.
Clearly, the answer is C.
To close all the steps, reload the exponent laws questions page